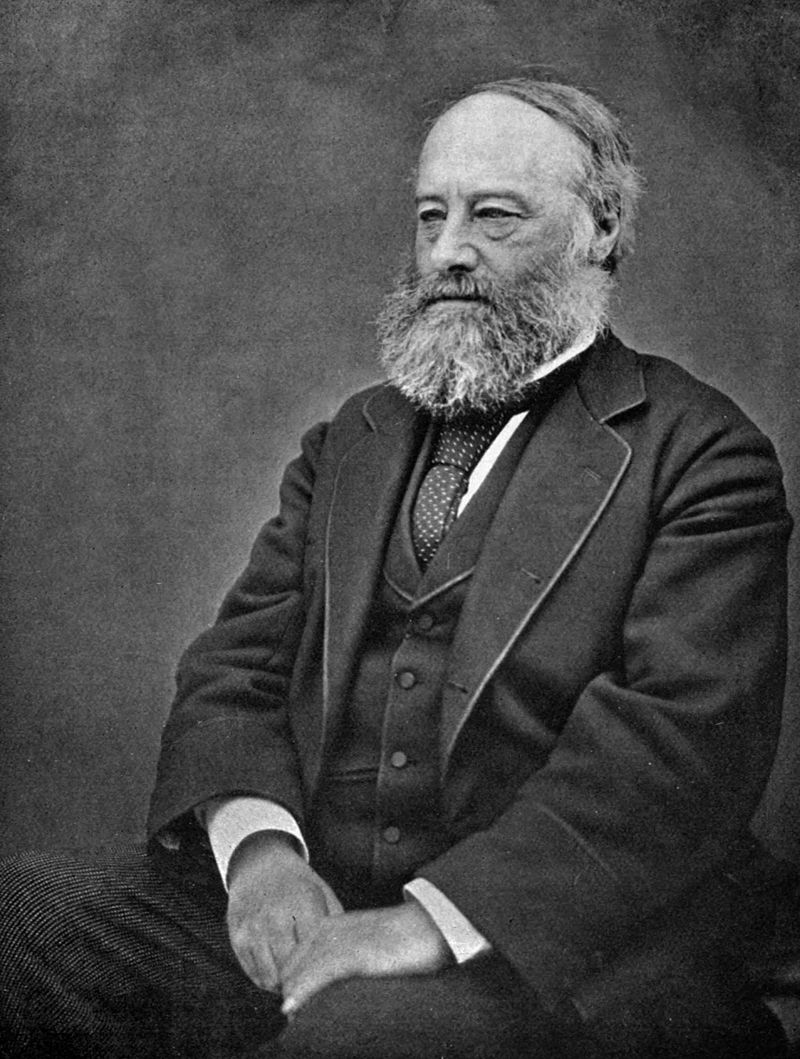units & tech

lunes, 11 de septiembre de 2017

CVF - Caballo Fiscal, Potencia Fiscal. ¿O porqué pago menos por mi nuevo coche con más CV?

Hace unos días recibí el impuesto de circulación de mi nuevo vehículo. Tiene algo más de un año, y, cuál fue mi sorpresa al compararlo con el recibo de este mismo año del antiguo coche, que..., ¡Tenía que pagar menos!. El impuesto venía en función de un valor calculado en CVF. - ¿Qué es el CVF? - me pregunté.

No conocía la unidad de medida CVF. Lo primero que me llegó a la mente fue: - Si CV se refiere a caballos, es decir, a la potencia del motor, y el coche nuevo tiene como 30 caballos más ¿cómo es posible que haya que pagar menos? -

Investigando un poco, en el caso de España, en efecto CVF se refiere a "Caballo fiscal" ó "Potencia fiscal", que es una unidad de medida que indica la carga impositiva que se le aplica a un vehículo en el municipio donde está registrado. Vamos, lo que coloquialmente se llama "Impuesto de circulación", o más formalmente impuesto sobre vehículos de tracción mecánica (IVTM) .

De modo que en función del valor obtenido al aplicar la fórmula, y el municipio donde esté registrado el vehículo, el valor del impuesto de circulación varía.

He visto que en el algunos municipios la unidad de medida la denominan "CF" (entiendo que caballo fiscal también), aunque no sé si es correcta esta abreviatura.

Pues bien, la fórmula para calcular el caballo fiscal depende, al menos en turismos, de una serie de características del motor del vehículo, en concreto, depende en gran medida de su cilindrada.

En el caso de España, está regulada por Real Decreto 2822/1998 del 23 de diciembre, en el Anexo V del Reglamento General de Vehículos.

Si sabemos que el volumen de un cilindro en centímetros cúbicos es:

Siendo:

D : Diámetro del cilindro en cm
R : Recorrido del pistón en cm

La cilindrada total del vehículo sera el volumen de un cilindro por el número de cilindros (suponiendo todos iguales):

Con lo cual la potencia fiscal, queda definida como:

Para simplificar, dado que no se suele conocer el diámetro del cilindro ni el recorrido del pistón, se utiliza el volumen total de los cilindros del motor, es decir, la cilindrada, que sí es un dato que aporta el fabricante. Así, la fórmula que se aplica, utiliza una constante T en función del tipo de motor, y queda en función del volumen en cm³, que sí se conocen:

Siendo:

Pf : Potencia fiscal
T : 0,08 para motores de cuatro tiempos, y 0,11 para motores de dos tiempos
C : Cilindrada del motor en cm³
N : Número de cilindros

Así, pude comprobar que mi nuevo vehículo, al tener un motor optimizado compacto de 998 cm³, entra en la categoría de hasta 8 CVF del impuesto de ciculación en mi municipio, mientras que el antiguo de unos 1600 cm³, entra en la siguiente categoría de entre 8 CVF y 11'99 CVF, que tiene una imposición mayor.

Es decir, que, aunque el nuevo vehículo incluya un motor capaz de aportar más potencia (más caballos), gracias a los avances en la ingeniería, es mucho más compacto, y con menos cilindros, con lo que, consigue reducir las emisiones, y, casualmente, su potencia fiscal entra en una categoría de menor imposición.

Se puede consultar las tablas de imposiciones a vehículos en el Ministerio de Hacienda y Función Pública del Gobierno de España, en este enlace.

Por último, comentar que, a nivel internacional se utiliza esta fórmula aún en algunos países, sobretodo en Europa, pero, en otros quedó desfasada o no se ha llegado a usar, dado que, no representa un valor conforme a la potencia real del motor.

Referencias:

- http://ingemecanica.com/tutoriales/cvf.html

- https://es.wikipedia.org/wiki/Caballo_fiscal

- http://www.autofacil.es/conductor/2014/08/06/paga-impuesto-circulacion/19823.html

- https://serviciostelematicos.minhap.gob.es/ConsultaTipos/aspx/listado_municipios.aspx?inicio=false
- https://en.wikipedia.org/wiki/Tax_horsepower

martes, 29 de agosto de 2017

A partir de 2018 cambia la definición de las unidades de medida por el S.I.

La próxima Conferencia General de Pesos y Medidas, se celebra del 13 al 18 de noviembre del próximo año 2018 en el Palacio de Congresos de Versalles, muy cerca de París, Francia, pasados cuatro años desde la anterior conferencia, que también se celebró en Versalles.

Se espera que esta nueva 26ª conferencia deje obsoletos muchos diccionarios y libros de texto, al redefinir las 7 unidades básicas del sistema internacional, en función de constantes físicas con valores revisados y corregidos, y su definición en función de otras unidades básicas, tambien definidas con ese mismo conjunto de constantes.

Existe un borrador oficial desde 2014, que se publicó en 2016 de las nuevas definiciones, constantes y relaciones.

Las constantes sobre las que se tiene previsto basar la definición de las 7 unidades básicas del Sistema Internacional son 7, de las que 4 se ha corregido su valor, y, ahora, todas tienen valores más precisos, considerados exactos (a fecha 29-08-2017):

Constante de Plank (corregida): h = 6,626070040×10⁻³⁴ kg·m²·s⁻¹
Carga eléctrica elemental (corregida): e = 1,6021766208×10⁻¹⁹ A·s
Constante de Bolzmann (corregida): k = 1,38064852×10⁻²³ kg·m²·K⁻¹·s⁻²
Constante de Avogadro (corregida): N_A = 6,022140857×10²³ mol⁻¹
Velocidad de la luz: c = 299792458 m·s⁻¹
Estado fundamental de transición hiperfina de frecuencia del átomo de cesio 133: Δν_Cs = Δν(¹³³Cs)_hfs = 9192631770 s⁻¹
Eficacia luminosa: K_cd = 683 cd·sr·s³·kg⁻¹·m⁻² . Siendo sr la unidad adimensional steradian, y cd la unidad candela.

Además se revisará la definición de kilogramo, amperio, kelvin y mol, para que estén basadas en la Constante de Avogadro.

Todos estos cambios, afectarán pues a la definición existente de las 7 unidades básicas del sistema internacional, mientras que las unidades derivadas del sistema internacional seguirán teniendo la misma definición.

De este modo se corrigen errores que existían en anteriores definiciones.

La nuevas definiciones propuestas ya en 2016 de las 7 unidades básicas del sistema internacional son (a fecha 29-08-2017):

Segundo: El segundo, símbolo s, es la unidad del SI de tiempo. Se define utilizando el valor numérico corregido de la frecuencia de cesio Δν_Cs , del estado fundamental impasible de transición hiperfina de frecuencia del átomo de cesio 133, 9192631770 expresado en la unidad Hz, que es igual a s⁻¹
Metro: El metro, símbolo m, es la unidad del SI de longitud. Se define utilizando el valor numérico corregido de la velocidad de la luz en el vacío c igual a 299792458 expresada en la unidad m·s⁻¹ , donde el segundo se define en términos de la frecuencia de cesio Δν_Cs
Kilogramo: El kilogramo, símbolo kg, es la unidad del SI de la masa. Se define utilizando el valor corregido de la constante de Planck 6,022140857×10²³ expresada en la unidad J·s, que es igual a kg·m²·s⁻¹ , donde el metro y el segundo de definen en términos de c y Δν_Cs
Amperio: El amperio, símbolo A, es la unidad del SI de la corriente eléctrica. Se define utilizando el valor numérico corregido de la carga eléctrica elemental e igual a 1,6021766208×10⁻¹⁹, expresada en la unidad C (Culombio), que es igual a A·s , donde el segundo se define en términos de Δν_Cs
Kelvin: El kelvin, símbolo K, es la unidad del SI de la temperatura termodinámica. Se define utilizando el valor numérico corregido de la constante de Bolzmann igual a 1,38064852×10⁻²³ cuando se expresa en J·K ⁻¹ , que es igual a kg·m²·K⁻¹·s⁻², siendo kilogramo, metro y segundo definidos en función de h, c, y Δν_Cs
Mol: El mol, símbolo mol, es la unidad de del SI de la cantidad de substancia de una entidad elemental específica, que puede ser un átomo, molécula, ion, electrón, otra partícula o grupo de dichas partículas especificadas. Se define tomando el valor numérico corregido de la constante de Avogadro N_Aigual a 6,022140857×10²³ expresada en la unidad mol⁻¹

Esta definición implica que cambia la relación entre dalton, masa de 12 átomos de carbono, kilogramo, y número de avogadro, que ya no es válida. Ahora la masa de 12 átomos de Carbono es 12 dalton.

Candela: La candela, símbolo cd, es la unidad del SI de la intensidad luminosa en una dirección dada. Se define utilizando el valor corregido de la eficacia luminosa de la radiación monocromática de frecuencia 540×10¹² Hz, K_cd , con valor 683 en unidades lm·W^-1 , o cd·sr·s³·kg⁻¹·m⁻² , donde el kilogramo, metro y segundo se definen en función de h, c, y Δν_Cs

Se puede ver que estos cambios y otros que se preveen debatir en la 26ª Conferencia General de Pesos y Medidas del año próximo, supondrán un paso hacia adelante en fortalecer la 7 pilares en que se basa todas las unidades de medida del sistema internacional, a costa de dejar obsoleta muchísima literatura de las últimas décadas.

NOTA: La información aquí recopilada y expuesta, a fecha de hoy 29-08-2017, es todavía una propuesta.

Referencias:
- http://www.bipm.org/en/worldwide-metrology/cgpm/
- https://en.wikipedia.org/wiki/Proposed_redefinition_of_SI_base_units

jueves, 24 de agosto de 2017

More than 100000 visits in this humble blog! Thank you!

Today, I've realized that this humble blog has exceeded the 100,000 visits counted.

¡¡¡Thanks for your visits!!!

I hope get more time to add new posts soon.

miércoles, 2 de agosto de 2017

Ohmio, Siemens, Amperio, Voltio, Culombio, Watio, Julio, Pascal, ... Algunas unidades en honor a científicos de siglos XVII, XVIII y XIX

Quienes hayan visto alguno de los capítulos de la serie Las Aventuras de Sherlock Holmes, de los años 80 del pasado siglo, deben haber disfrutado con la buena recreación de la Inglaterra del siglo XIX, y quizá extrapolable en muchos aspectos al siglo XVIII.

Fué durante estos siglos que la ciencia empezaba a dar firmes pasos hacia adelante, con multitud de descubrimientos y nuevas ramas del saber que iban surgiendo, como la electricidad o la química.

Es curioso el caso de Henry Cavendish, un grandísimo científico inglés de la London's scentific society, que se cree tenía el Síndrome de Asperger, y, aunque hizo grandes avances en la química, física, o la electricidad, casi no publicó ninguno de sus trabajos, de modo que muchos de sus descubrimientos fueron posteriormente realizados y atribuidos a otros, hasta que fueron descubiertas las notas y documentos que había dejado en su casa años después de su muerte.

Son muchos los científicos que propiciaron estos avances durante los siglos XVII, XVIII y XIX. En el campo de la electricidad podemos destacar los siguientes:

Sir Isaac Newton
Benjamin Franklin
Humphry Davy
Sir Joseph Wilson Swan
Charles Francis Brush
Thomas Alva Edison
Georg Simon Ohm
James Watt
Henry Bell
Thomas Davenport
Alessandro Giuseppe Antonio Anastasio Volta
Gaston Plante
Alexander Graham Bell
Lewis Howard Latimer
Georges Leclanché
Nikola Tesla
Roentgen, Wilhelm Vom
James Clerk Maxwell
Henry Cavendish
William Thomson
Charles-Augustin de Coulomb
Ernst Werner von Siemen
James Prescott Joule
André-Marie Ampère

Y del mismo modo se podrían enumerar grandes científicos para los campos de las matemáticas, química, u otros campos que iban surgiendo de la física.

Estos avances, surgidos gracias a una base matemática, que iba unos pasos por delante, fueron "el material de construcción" de multitud de posteriores descubrimientos e inventos, que aún hoy en día se producen.

Surgían nuevos conceptos matemáticos, físicos, y químicos que debían poderse medir, y con ello surgían nuevas unidades de medida, con más o menos precisión y acierto.

En 1861, Latimer Clark, y Sir Charles Bright presentaron un paper sugiriendo que debían establecerse estándares para las unidades eléctricas, y proponiendo nombres de eminentes filósofos o físicos: "Ohma", "Farad", "Volt".

Para el caso del Ohmio, en 1861, la British Association for the Advancement of Science, junto con William Thomson y James Clerk Maxwell, decidieron que debían establecer una unidad de medida para la resistencia eléctrica, y que formase parte de un sistema coherente de medidas para la electricidad. No fue hasta 1867, que se definió como Ohm, y, William Henry Preece sugirió el símbolo Ω. Pues bien, no fue hasta 1990 en la 18ª Conferencia General de Pesos y medidas, que se estableció una nueva definición más precisa para medirlo. Abajo se listan unidades alternativas que se usaron para medir la resistencia:

Unidad	Definición	Valor en British Association (B.A.) "ohm"	Información
Absolute foot/second × 10⁷	usando Imperial units	0.3048	considerada obsoleta incluso en 1884
Thomson's unit	usando Imperial units	0.3202	100 million feet/second, considerada obsoleta incluso en 1884
Jacobi copper unit	Un cable de cobre específico de 25 pies de largo y peso 345 granos	0.6367	Usada en los 1850s
Weber's absolute unit × 10⁷	Basada en el metro y el segundo	0.9191
Siemens mercury unit	1860. Una columna de mercurio puro	0.9537	100 cm and 1 mm² sección transversal a 0 °C
British Association (B.A.) "ohm"	1863	1.000	bobinas estándar depositadas en el observatorio de Kew en 1863
Digney, Breguet, Swiss		9.266–10.420	Alambre de hierro de 1 km de largo y 4 mm cuadrados de sección trasversal
Matthiessen		13.59	Una milla de alambre de cobre recocido duro a 15,5 ºC de 1/16 pulgada de diámetro
Varley		25.61	Una milla de alambre de cobre especial de 1/16 pulgadas de diámetro
German mile		57.44	Una milla alemana (8,238 yard) de alambre de hierro de 1/6 pulgadas de diámetro
Abohm		10−⁹	Unidad electromagnética absoluta en unidades centímetro-gramo-segundo (cgs)
Statohm		8.987551787 × 10¹¹	Unidad absoluta electrostática en unidades de centímetros-gramos-segundo (cgs)

Hoy en día, según el S.I.:

$\Omega ={\dfrac {\text{V}}{\text{A}}}={\dfrac {1}{\text{S}}}={\dfrac {\text{W}}{{\text{A}}^{2}}}={\dfrac {{\text{V}}^{2}}{\text{W}}}={\dfrac {\text{s}}{\text{F}}}={\dfrac {{\text{J}}{\cdot }{\text{s}}}{{\text{C}}^{2}}}={\dfrac {{\text{kg}}{\cdot }{\text{m}}^{2}}{{\text{s}}{\cdot }{\text{C}}^{2}}}={\dfrac {\text{J}}{{\text{s}}{\cdot }{\text{A}}^{2}}}={\dfrac {{\text{kg}}{\cdot }{\text{m}}^{2}}{{\text{s}}^{3}{\cdot }{\text{A}}^{2}}}$

Para el caso del Voltio (V), el nombre propuesto fue en honor a Alessandro Volta, que por 1800, junto a Luigi Galvani desarrolló la pila voltaica. Pero no fue hasta 1881, cuando el International Electrical Congress, aprobó dicho nombre como unidad de medidad para la fuerza electromotriz (hoy en día la definición es el diferencial de voltage de un conductor cuando se le aplica un amperio y disipa un watio de potencia). De modo que 1 voltio (V) era equivalente a 10⁸ unidades cgs de voltage, que era aproximadamente la fuerza electromotriz (emf) de una pila Daniell, utilizada para los sistemas telegráficos de la época.

El sistema cgs (centímetros-gramos-segundo) era una unidad de medida utilizada en la época.

1 V ≈ 10⁸ cgs

Hoy en dia, según el S.I.:

${\text{V}}={\frac {\text{potential energy}}{\text{charge}}}={\frac {{\text{N}}{\cdot }{\text{m}}}{\text{C}}}={\frac {{\text{m}}{\cdot }{\text{kg}}{\cdot }{\text{m}}}{{\text{A}}{\cdot }{\text{s}}{\cdot }{\text{s}}^{2}}}={\frac {{\text{kg}}{\cdot }{\text{m}}^{2}}{{\text{A}}{\cdot }{\text{s}}^{3}}}.$

${\text{V}}={\text{A}}{\cdot }\Omega ={\frac {\text{W}}{\text{A}}}={\frac {\text{J}}{\text{C}}}={\frac {\text{eV}}{e}}.$

Alessandro Volta

Para el caso del Amperio (A), se definió como una de las unidades de la corriente eléctrica en unidades cgs ( antigua unidad conocida como abampere(abA) ).

Antigua definición: 1 A ≈ cantidad de corriente que genera una fuerza de 2 dyn por centímetro entre dos cables separados 1 centímetro.

dyn (dina) es una antigua unidad de medida de fuerza en el sistema cgs.

1 dyn = 1 g⋅cm/s²nbsp;= 10⁻⁵ kg⋅m/s² = 10⁻⁵ N

Con el paso del tiempo se quedó obsoleta dicha definición de amperio y se establecieron otras más precisas.

Hoy en día según el S.I.:

${\rm {1\ A=1{\tfrac {C}{s}}.}}$

Su nombre fue en honor del matemático y físico francés André-Marie Ampère por los aportes en la electrodinámica.

André-Marie Ampère

Para el caso Culombio (C), el nombre fue en honor de Charles Coulomb, que aportó importantes avances en la física, como la definición de fuerza electrostática, avances en el campo de la fricción, la ley de Coulomb (que describe la fuerza que interacciona entre partículas estáticas cargadas elécticamente), etc.

Según el S.I.:

$1~{\text{C}}=1~{\text{A}}\cdot 1~{\text{s}}$

que es equivalente a:

$1~{\text{C}}=1~{\text{F}}\cdot 1~{\text{V}}$

Charles-Augustin de Coulomb

Para el caso de Siemens (S), es una unidad derivada que se definió ya en en 1971, en la 14 Conferencia General de Pesos y Medidas, y su nombre fue en honor del Ernst Werner von Siemens, quien fue un inventor e industrial alemán, fundador de la empresa de telecomunicaciones Siemens, y que tubo diversas de patentes relacionadas con medidas eléctricas.

En 1860 definió la unidad de medida Siemens mercury unit, para la resistencia eléctrica, aunque pasó a considerarse obsoleta en 1884, y no fue reconocida por el SI.

1 Siemens mercury unit ≈ 0'953 Ω

En 1881, otra unidad denominada siemens, se definió en el sistema métrico ( reconocida en el S.I. ) como unidad derivada de resistencia y conductancia eléctrica, susceptancia eléctrica, y admitancia eléctrica.

En conductancia, G = S:

$\mathrm{S} = \Omega^{-1} = \dfrac{\mathrm{A}}{\mathrm{V}}$

Ernst Werner von Siemens

Debido a que es la inversa del ohmio, un nombre alternativo que se propuso antes de siemens fue mho (℧).

Para el caso de Watio (W), el nombre lo dió el propio inventor, en este caso el escocés James Watt, en sus contribuciones en la máquina de vapor. Fue adoptada en 1882 para usarla en la medición de energía producida por agua y carbón, y en 1960, la 11a Conferencia de Pesos y Medidas la adoptó para la medición de la potencia en el SI, como unidad derivada.

$\mathrm {1~W=1~{\frac {J}{s}}=1~{\frac {N\cdot m}{s}}=1~{\frac {kg\cdot m^{2}}{s^{3}}}}$

$\mathrm {1~W=1~V\cdot A}$

$\mathrm {1~W=1~{\frac {V^{2}}{\Omega }}=1~A^{2}\cdot \Omega }$

James Watt

Para el caso del Julio (J), se nombró en honor al físico y matemático inglés James Prescott Joule, por sus aportes a la mecánica del calor, mediciones muy precisas de resistencias, teoría cinética, etc.

El Julio es una unidad derivada, reconocida por el S.I. definida como:

${\text{J}}={\frac {{\text{kg}}\cdot {\text{m}}^{2}}{{\text{s}}^{2}}}={\text{N}}\cdot {\text{m}}={\text{Pa}}\cdot {\text{m}}^{3}={\text{W}}\cdot {\text{s}}={\text{C}}\cdot {\text{V}},$

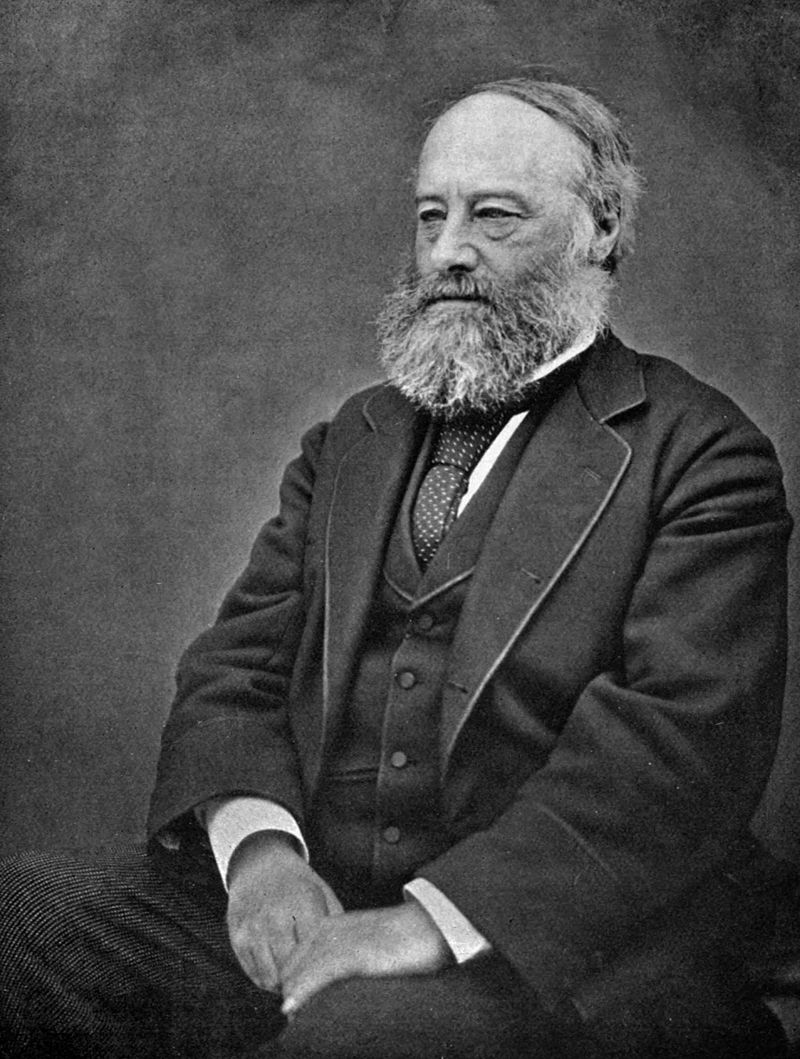James Prescott Joule

Para el caso del Newton (N), la unidad de medida se nombró en honor a Isaac Newton, un matemático, astrónomo y físico/"filósofo natural" que contribuyó en muchos campos de las matemáticas y la física.

El Newton es una unidad derivada de la fuerza, reconocida y adoptada en 1946 por el antiguo sistema de unidades MKS (sucesor del antiguo sistema de unidades cgs), y en 1948 por el nuevo Sistema Internacional de Unidades como Newton.

Conforme la 2ª Ley de Newton, o ley fundamental de la dinámica:

- Si la masa es constante:

$\sum \mathbf {F} =m\mathbf {a}$

- Si la masa no es constante:

$\mathbf {F} _{\rm {neta}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}$

Así se obtiene que 1 Newton es:

${\rm {1\,N=1\;{{kg\cdot m} \over s^{2}}}}$

La equivalencia con la antigua unidad de medida dina, del sistema cgs (sistema cegesimal) es:

1 N = 10⁵ dinas

Isaac Newton

Para el caso del Pascal (Pa), el nombre de Pascal se puso en honor a Blaise Pascal, un matemático, físico, inventor, escritor y teólogo católico francés del siglo XVII, que durante su corta vida, realizó importantes contribuciones en el campo de los fluidos, y aclaró los conceptos de presión y vacío. Fue un importante inventor, creando calculadoras mecánicas, y un importante matemático, ampliando los campos de la geometría proyectiva y la teoría de la probabilidad.

Blaise Pascal

Por todo ello, en la 14a Conferencia General de Pesos y Medidas de 1971, se adoptó en su nombre la unidad de medida Pascal para medir presiones, es decir, cuantificar presiones internas, estrés mecánico, Módulo de Young (relacionado con la elasticidad), y tensiones de rotura (capacidad de un material o estructura de soportar cargas de presión de deformación).

${\rm {1~Pa=1~{\frac {N}{m^{2}}}=1~{\frac {kg}{m\cdot s^{2}}}}}$

Aunque la unidad de medida por el Sistema Internacional para la presión es el Pascal, se sigue utilizando mucho otra medida que se adoptó en 1954, en la 10a Conferencia general de pesos y medidas, que es la atmósfera (atm), y que hoy en día ha sido reconocida por diferentes ISO, para utilizarla en diferentes campos:

ISO 2787 (herramientas neumáticas y compresores)

ISO 2533 (uso aeroespacial)

ISO 5024 (en petróleo)

De modo que es frecuente escuchar o leer en diferentes campos (como en los partes del tiempo), la unidad atm en vez del Pascal.

1 atm ≈ 101325 Pa

Incluso es posible leer o escuchar otra unidad de medida más antigua (posiblemente de la época Griega) para la presión, y no reconocida ni por ISO ni por el SI, que son el bar .

1 bar ≈ 0,987 atm

1 bar ≈ 100000 Pa = 100000 N/m²

En este otro post se puede leer más información de la unidad Pascal y relación con otras unidades de medida de presión, algunas obsoletas.

-------------

Referencias:

- https://en.wikipedia.org/wiki/Ohm

- https://es.wikipedia.org/wiki/Ohmio

- La medida de todas las cosas, 2009

domingo, 25 de diciembre de 2016

asu, dBm

Recuerdo hace más de 3 años, enredando con mi antiguo móvil, que ví la unidad de medida "asu" para referirse a la intensidad de la señal de telefonía.

asu es el acrónimo de "Arbitrary Strength Unit", y es un valor entero proporcional a la fortaleza de la señal recibida.

Es posible calcular la potencia de la señal en dBm (tb. dBmW ó decibelios-milivatio) a partir del valor "asu".

Según el tipo de red telefónica (GSM / GPRS / EDGE, UMTS / HSDPA / HSPA+ , LTE, etc.) que esté usando la antena del dispositivo, el rango de valores posibles para asu varía, así como varía la fórmula de conversión de asu en dBm.

En los enlaces de referencia se puede consultar más información sobre los rangos y conversiones.

dBm es una unidad de medida absoluta, que se utiliza para indicar la potencia absoluta expresada en decibelios (dB) medida en un milivatio (mW)

{\begin{aligned}x&=10\log _{{10}}{\frac {P}{1{\mathrm {mW}}}}\end{aligned}}

Conversión de potencia en mW a dBm

En mi móvil actual con Android 5.1.1, se puede ver consultando "Acerca del dispositivo" > "Estado" diferentes valores, entre ellos la "Intensidad de la señal", medida en dBm, y en asu .

Referencias:

- https://en.wikipedia.org/wiki/Mobile_phone_signal#ASU
- http://www.lte-anbieter.info/technik/asu.php
- https://es.wikipedia.org/wiki/DBm

sábado, 17 de diciembre de 2016

em, x-height, ex, en, rem, typographic point, DTP point

Last year's summer I was modifying the design of a web page for make it more "responsive" (adjustable to different resolutions and sizes for web browsers of diferent devices: mobile, laptop, pc, tablet). Reading about this for HTML 5 with CSS (Cascading Stylesheets) 3, I found an interesting measure unit, that I thought that I should write a post about it: the em.

em is a relative (and scalable) measure unit, that represents the value of the width of the M letter (upper case em letter) in the current typeface and point size.

Traditionally, in printing presses, the M was commonly cast the full-width of the square blocks, or em-quads.

The fact that M is commonly the full-width, it's why em is usually represented as a decimal value less than 1 in web designing (e.g., 0.7 em), or as fractions (e.g., 70/100 em .

An algorithm that have to play CSS with em must do a mathematical calculation accoring the points of the typography. For example: a typography of 12 points, 1 em = 12 points.

By default, 1 em = 16 points ( 16 points - typeface ).

In computing, in CSS, the rem or root em, is the font size of the root element of the document, and is constant throughout it; not like the em, which may be different for each element.

A similar measure unit in typography to em is the "x-height", that refers to the distance between the baseline and the mean line of the lower-case letters in a typeface. Typically, this is the height of the letter x in the font.

In computing, in CSS and LaTeX, the x-height is called ex , and the exact ratio of ex to em can vary (aprox. 1 ex = 0.4 - 0.5 em) by font size within a browser according the rounding.

In typography, an en is another measure unit, that represents half of the width of an em, and supposed the width of the uppercase letter "N" . ( 1 en = 0.5 em ) . By default, 1 en = 8 points.

We've seen that this meause units are referred to the point, more exactly the "typographic point". This is the smallest unit of measure in typography, and it's used for measuring font size, leading, and other items on a printed page.

The size of the point has varied throughout the history of printing. Since the 18th century, the point's size has varied from 0.18 to 0.4 millimeters.

Traditionally, in metal type, the point size of the font described the height of the metal body on which the typeface's characters were cast.

The point was first established by the Milanese typographer, Francesco Torniella da Novara (c.1490 – 1589) in his 1517 alphabet, L'Alfabeto. The construction of the alphabet is the first based on logical measurement called "Punto," which corresponds to the ninth part of the height of the letters or the thickness of the the principal stroke.

1 point in ...	... is equal to ...
typographic units	1/12 picas
imperial/US units	1/72 in
metric (SI) units	0.3528 mm

For more point definitions and equivalences along the histoy, access to this link.

Fournier's printed scale of his point system, from Manuel Typographique, Barbou, Paris 1764, enlarged.

Since 1980s, the digital printing has largely supplanted the letterpress printing and has established the DTP point (desktop publishing point or PostScript point) as the facto standard.

The DTP point is defined as ¹⁄₇₂ of an international inch (about 0.353 mm) and, as with earlier American point sizes, is considered to be ¹⁄₁₂ of a pica:

12 points = 1 pica . 6 pica = 1 international inch

In 1996, it was adopted by the W3C (World Wide Web Consortium) for CSS, where it was later related at a fixed 4:3 ratio to the pixel due to a general (but wrong) assumption of 96 px / in screens.

The notation of measurement in typographic points can be represented in different ways. For example 16 points can be written in:

Traditional sytle: 1P̸4p (1 pica plus 4 points). Where 1 pica = 1P̸ = 12 points.
Desktop style: 1p4 (1 pica plus 4 points). Where 1 pica = 1p = 12 points.
CSS defined by the W3C: 16 pt. Where 1 pt = 1 pc = 1 pica .

References:

- https://librosweb.es/libro/css/capitulo_3/unidades_de_medida.html

- https://es.wikipedia.org/wiki/Em_(tipograf%C3%ADa)

- https://en.wikipedia.org/wiki/Em_(typography)

- https://en.wikipedia.org/wiki/X-height

- https://en.wikipedia.org/wiki/Point_(typography)

martes, 6 de diciembre de 2016

Barcella

Pot ser la majoria de les persones que hem caminat per la Plaça de la Reina, açí a València, ens hem fixat en l'antic arc que uneix la Catedral de València i el Palau Episcopal, i pot ser no sapiem el nom del carrer on està aquest arc, ni ens hàgem fixat en la pedra a la paret que hi ha quasi sota l'arc.

El carrer rep el nom per l'arc, i l'arc rep el nom per aquesta antiga pedra romana, que representa la unitat "oficial" de mesura "barcella" en les transaccions comercials des de l' època romana fins que aparegueren les unitats internacionals de mesura que la reemplaçarien.

Com no existía un únic criteri per a aquesta unitat de mesura, ficaren aquesta pedra amb la referència per a les transaccions en l'antiga ciutat de València, ben a prop dels principals carrers on es comerciava amb farina, blat, cereals, ...

Una barcella és una antiga mesura volumètrica de gra que equival aproximadament a la sisena part d'una quartera. A les Illes Balears es divideix en sis almuds; a la regió de València, en quatre almuds.

Una barcella és també el recipient que té la capacitat de dita mesura i serveix per a mesurar.

També barcella es pot referir a l'extensió de terra de prou capacitat per sembrar-hi una barcella de gra.

En castellà: "barcilla" .

Utilitzada a l'antic Regne de València, les equivalències diferien segons el lloc on s'usava:

A terres Valencianes: 1 fanega = 2 barcelles
1 barcella = 4 almuds
En Balears: 1 barcella = 6 almuds

1 barcella = 1/12 cafiç

En Alacant: 1 barcella = 4 celemins (≈ 20.75 litres)
En Castelló de la Plana: 1 barcella ≈ 16,6 litres
En Morella: 2 mitges barcelles ≈ 8 mesures
En València: 1 barcella ≈ 16,75 litres

Com a unitat de mesura utilitzada al Regne de València, es poden trobar antics dits de justícia, lleis, ordenaments, resolucions judicials, etc. que fan referència a aquesta unitat. Per exemple, al "Llibre d'establiments i ordenacions de la ciutat de València" (1296 - 1345), podem trobar multitud de referències com la següent:

"... Encara hondenaren que nengú dels dits tenders o tenderes, ne alcuna altra persona, de vuy a avant no gos fraudulentment fer metre nous una a una en la barcella, ne encara maestrívolment fer curumullar ab les dites nous alcuna barcella o barcelles e enaprés, segons aquesta barcella o barcelles axí fraudulentment feites ..."

Referències:

- http://dcvb.iecat.net/
- http://dicter.usal.es/lema/barcella
- https://mateturismo.wordpress.com/2013/09/02/piedra-de-la-barchilla-en-valencia/
- http://www.lasprovincias.es/v/20101121/valencia/barcilla-para-medir-20101121.html
- Llibre d'establiments i ordenacions de la ciutat de València (1296 - 1345)

domingo, 28 de agosto de 2016

Unidad de masa atómica unificada - Dalton

Leer el nombre de Dalton me lleva a la época de pequeño que veía la serie animada western "Lucky luke", en la que un vaquero solitario, su caballo y un perro incomprendido resolvían distintos tipos de delitos, atrapaban a los malos, etc. Los hermanos Dalton eran 4 personajes de la serie que intentaban conseguir dinero por malas artes, y por lo general siempre acababan en la cárcel.

Si en vez de Dalton lees Daltonismo, te viene a la mente esa enfermedad que te enseñan en el colegio, que tienen algunas personas, que no pueden distinguir bien ciertos colores.

Lo que no me esperaba era encontrar "Dalton" como una unidad de medida. Y eso sucedió, no hace mucho, cuando leí en una noticia científica la unidad de medida "Unidad de Masa Atómica Unificada", también llamada "Dalton".

Resulta que tanto la unidad de medida, como el daltonismo vienen en honor a la misma persona, John Dalton, un químico, físico, y metereólogo inglés, que vivió entre los siglos XVIII y XIX, y que tenía una enfermedad visual, que describió por primera vez sus causas; así como sugirió por primera vez en 1803 que, en la escala de masa atómica relativa (peso atómico), la primera masa relativa atómica fuese la del Hidrógeno.

John Dalton

Se sabe que ya en el siglo V a.C., existía una teoría atomista de la materia (la materia está formada por átomos) por parte de los griegos.

Esta idea se recuperó con la revolución científica de los siglos XVII y XVIII, y se intensificó con la teoría cuántica en el siglo XX.

En el siglo XIX se acumularon pruebas de la existencia de átomos y moléculas, y John Dalton fue el primero que definió el átomo como la parte más pequeña de una sustancia que podía participar en una reacción química. Y el primero en publicar una tabla de pesos atómicos relativos (solo tenía 6 elementos: hidrógeno, oxígeno, nitrógeno, carbono, azufre y fósforo), basada en estas premisas:

Los elementos están formados por pequeñísimas partículas llamadas átomos.
Átomos de un elemento dado tienen idéntico tamaño, masa y propiedades; y difieren de otro elementos.
Los átomos no se pueden subdividir, crear o destruir.
Átomos de diferentes elementos se combinan en un conjunto reducido de proporciones para formar compuestos químicos.
En reacciones químicas, los átomos se combinan, separan, y reorganizan.

Y en la idea anterior, que el átomo de hidrógeno es el peso de una unidad.

John Dalton hizo avances científicos en diferentes campos, y, al igual que el Daltonismo como enfermedad visual lleva su nombre, y que hoy en día se conocen diferentes grados, y que él en realidad lo que tenía era "deuteranopia"; la unidad de masa atómica unificada ( u ) , también se le llama "Dalton" ( Da ) en su nombre, por todos los descubrimientos que hizo en ese campo de la ciencia.

Hoy en día 1 Da es una unidad estándar que se usa para indicar la masa a escalas atómicas o moleculares. Y es aproximadamente la masa de un nucleón (protón o neutrón).

El Comité Internacional de Pesos y Medidas, la considera una unidad que no pertenece al Sistema Internacional de Unidades (SI) , pero que acepta utilizarla con el SI, calculando experimentalmente el valor.

El Sistema Internacional de Magnitudes (ISO 80000-1:2009) define que el nombre correcto es "Dalton", y desaconseja llamarla "unidad de masa atómica unificada" (nombre anticuado), ya que puede adoptar dos valores distintos (ISO 80000-1:2009 y ISO 80000-10:2009) y, además, no admite prefijos multiplicativos.

En 1961 la unidad de medida "unidad de masa atómica" (amu) (sin el prefijo unificada), pasó a considerarse obsoleta, basada en el oxígeno. Hoy en día en algunos textos se la intenta tratar amu como u, por lo que puede ser confuso si no se especifica si está basada en el Carbono-12 o en el Oxígeno-16.

En 1993, la Union of Pure and Applied Chemistry aprobó el uso de la unidad dalton.

Definición:

1 Da = 1/12 (la doceava parte) de la masa de un átomo, neutro y no enlazado de Carbono-12. (Unidad de medida No-SI).

Equivalencias:

1 Da = 1 u
1 u = m_u = (1/12) m (¹²C)
1 átomo de Carbono-12 tiene una masa de 12 u (12 Da)

1 átomo de Hidrógeno-1 tiene una masa de ≈ 1,0078250 u = 1,0078250 Da
La tinina, la proteína más grande conocida, tiene una masa molecular de 3 - 3,7 MDa (Megadaltons)

Equivalencias con el SI:

1 Da ≈ 1,660538921(73) × 10⁻²⁷ kg
1 Da ≈ 931,4940954(57) MeV/c² (Megaelectrónvoltio)
1 Da ≈ 1822,88839 m_e (electrón)
N_A (12 u) = 0.012 kg/mol (N_A : Número de Avogadro)
N_A (1 u) = 0.01 kg/mol (N_A : Número de Avogadro)

Bibliografía
- https://es.wikipedia.org/wiki/John_Dalton
- https://es.wikipedia.org/wiki/Unidad_de_masa_at%C3%B3mica
- https://en.wikipedia.org/wiki/Unified_atomic_mass_unit
- https://en.wikipedia.org/wiki/International_System_of_Units
- Metrum, 2007

viernes, 13 de mayo de 2016

My Organic Garden

I've been interested in farming since I was a child, when I heard histories about the life of my parents, grandparents, and ancestors in their small spanish villages before emigrate to live in a better place.

I've been experimenting with grow edible plants in pots since I was in school, and now, with the new movements of urban and organic crops, I decided to try, and rent an small parcel for growing some edible, aromatic, and culinary plants for learning about the agriculture, and consumption some organic vegetables.

I started more than a year ago, and I've experimented with many different edible and aromatic plants.

I've got many edible pepper, tomatoes, onions, lettuces, carrots, beans, ....

Now, starts the second year, with the spring-summer crops, and continue experimenting with different varieties and products.

I'm not sure how much time will be with this extra dedication, but meanwhile, I'll continue uploading photos of the garden and the harvests.

Page where I upload photos of my 2016 organic garden.

And, some photos of the 2015 in this page .

sábado, 19 de septiembre de 2015

Tweets, TPS, ...

Today is presented the new Twitter account for this blog: @uatblog

I don't have much time to attend it, so it will be an experiment for a while.

In this post I'm going to talk about the "tweet" (or maybe better "tweets") as a new "in fact" measure unit used widely in messages, press, and by the young people around the world.

A Tweet is a chirping note made, supposed by a bird, and, nowadays is also the sort message - until 140 characters - that can be sent through the Twitter platform.

A Tweet can also include multimedia data: image, video, ... But people - I think - associates it to a short message sent through this platform.

Somethig that started as a brainstorming idea / startup / internal project of a company, nowaday is a widely used tool around the world, with lot of new features unthinkable in those days.

The money, globalization and new technologies that rules our socities have a great source of data (as a datawarehouse) feed continuously that can be used to analyze with data mining and business intelligence techniques and technologies.

Nowadays there are many robots (as a software applications) that use the tweets to analyze for example the socity of a city, election results, fashion tendencies, sport team supporters, ....

Tweets are managed along the time, and new derived measueres have appeared: like TPS (Tweets per second), TPM (Tweets per minute), TPH (Tweets per hour), TPD (Tweets per day), ...

References:

- https://en.wikipedia.org/wiki/Twitter

- https://blog.twitter.com/2013/new-tweets-per-second-record-and-how

- https://twitter.com/twitterdata/status/425127921657724928

sábado, 23 de mayo de 2015

Codo árabe de Omar

No consigo sacar tiempo para el blog y se me van a acumulando las entradas pendientes de escribir...

Hace unos meses vi un programa muy bueno sobre una de las maravillas arquitectónicas más impresionantes de la civilización, situada en la Península Ibérica, la Alhambra de Granada.

La humanidad a lo largo de la historia tiende a crear grandes construcciones y monumentos que perduren entre las generaciones venideras, y que sirvan de algún modo de recuerdo de aquello que llegó a ser la cultura y la situación política y social en aquel lugar, al menos en aquellos casos de máxima representación. La Alhambra de Granada es un ejemplo de ello.

Plano de los Palacios nazaries y de las Habitaciones del Emperador.
Alhambra de Granada.

Hoy en día sigue sorprendiendo el nivel arquitectónico y artístico de la Alhambra de Granada, resultado de diferentes reformas y ampliaciones a lo largo del tiempo.

Una de las cosas que me llamó la atención, y por la que escribo este blog, es la unidad de medida que se utilizó: el Codo Árabe de Omar .

Por lo que he leído, parece ser que el origen está en unas construcciones militares defensivas aprovechando las vistas de la colina sobre la que se asienta, se fue ampliando según necesidades militares, pero no fue hasta que se erigió como palacio, cuando se produjo el gran cambio arquitectónico.

He hablado en otros posts sobre las medidas antropomórficas, previas a las unidades del sistema internacional, y, el Codo Árabe de Omar, es una de ellas.

El codo (en sus diferentes variantes), como unidad de medida, ha sido utilizado durante centenares de años (quizá miles) para cubrir diferentes necesidades humanas.

Por lo general, un codo era la distancia que mediaba entre el codo y el final de la mano abierta (codo real) o a puño cerrado (codo vulgar). Lógicamente, su valor variaba de un país a otro, inclusive dentro del país, según su uso.

Es difícil que dos personas tengan la misma longitud de codo, y por ello difícil que piezas de construcción elaboradas por diferentes personas de la época pudiesen cuadrar sin problemas. Aun así, muchas grandes construcciones se elaboraron con este tipo de medidas, y La Alhambra fue una de ellas.

Buscando la equivalencia en metros encuentro muchas variantes de codo árabe, codo de castilla, codo egipcio, codo romano, codo persa, ....

El codo árabe de Omar parece que medía sobre los 0'64 m.

Leo: "... Para crear un espacio que sobrecogiera a los visitantes con la importancia de su sultán, los arquitectos de Yusuf diseñaron una planta de 18 codos cuadrados, dividieron la sala a lo largo de sus ejes horizontal y diagonal, y posteriormente, utilizaron cuerda y lápiz para trazar cuatro arcos de 90 grados de pared a pared. Trazaron una línea recta entre los extremos de estos arcos para crear un octágono que a su vez permitió crear un cuadrado más grande situado en diagonal con respecto al original y que marca la ubicación de las ventanas centrales de la entrada.
Los triángulos equiláteros trazados desde el centro de las paredes crean estas ventanas de anchura perfectamente proporcional. ..."

Esto es un ejemplo de la profesionalidad de aquellos albañiles, constructores y arquitectos que participaron en su construcción.

Referencias:
- http://es.wikipedia.org/wiki/Codo_(unidad_de_longitud)
- http://www.alhambra-entradas.com/alhambra-granada.html
- Medición del Codo Árabe de Omar

domingo, 4 de enero de 2015

More than 1000 visits last month! Thank you!

Today this blog has passed the 1000 visits for the last month. It's a great quantity for a small non-profit blog without relevant neither important information.

¡¡¡¡Thanks for your visits!!!!

Visits to units&tech blog at 23:53 04-01-2015

Visits to units&tech blog at 00:00 16-01-2015